8 класс

Задача 1.  На берегу реки расположены пункты А и В. Определите среднюю скорость vср катера при движении от пункта А к пункту В и обратно, если собственная скорость катера v =10 км/ч, а скорость течения реки u = 2 км/ч.

Решение. Обозначим S – расстояние между пунктами А и В.
Время движения из пункта А в пункт В:  .                   2 балла
Время движения обратно   .                                           2 балла    
Средняя скорость катера при движении от пункта А к пункту В и обратно
 .                                                 6 баллов

Задача 2. В U – образную трубку налили жидкость плотности ?0 = 1,2 г/см3.Затем в левое колено налили воду плотности ?1 = 1,0 г/см3 , а в правое колено – масло плотности ?2 = 0,9 г/см3 . Высота столбика воды составляет h1 = 24 см, высота столбика масла – h2 = 20 cм. Найдите разность уровней воды и масла в коленах трубки, если жидкости не перемешиваются.

Решение. Определим давление, оказываемое столбами воды и масла в коленах трубки: .               2 балла
Так как p1  >  p2, то вода будет выдавливать жидкость плотности ?0 из левого колена в правое.                                                                              1 балл
Из условия равновесия жидкостей в коленах трубки
                                                                          2 балла
найдем высоту столба жидкости ?0, находящуюся выше нижнего уровня воды   = 5 см.                                                            2 балла
Разность верхних уровней воды и масла
, уровень масла выше .                                   3 балла

Задача 3. Гидравлический пресс с двумя поршнями разного диаметра закреплен на бетонном полу в цехе. К штокам поршней прижаты два одинаковых ящика. Минимальная сила, которую нужно приложить к левому ящику, чтобы сдвинуть оба ящика вправо, составляет F1.
Аналогично , к правому ящику необходимо приложить силу не меньше F2, чтобы сдвинуть оба ящика влево. Какую минимальную силу F необходимо приложить к точно такому же отдельно стоящему ящику, чтобы сдвинуть его с места? Учитывайте трение только между ящиками и полом.

Решение. Чтобы сдвинуть ящик с места, нужно преодолеть силу трения Fтр.
В первом опыте
,                                               2 балла
где силы и давлений на левый и правый поршни соответственно связаны соотношением 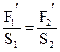,                                              1 балл
где S1 и S2 – площади левого и правого поршней соответственно.
Аналогично, для второго опыта (когда сила действует справа), имеем:
.                                                           2 балла
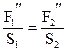  .                                                                            1 балл     
Из записанных уравнений найдем:
         
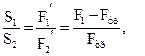
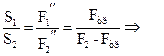
   .                                                                4 балла    

Задача 4. Если в калориметр со льдом при температуре t1 = -200C опустить металлический брусок, то растает 2/3 льда. Если после этого в калориметр опустить еще один такой же брусок, то установится температура t2 = 150C. 
Определите первоначальную температуру брусков, имеющих одинаковую температуру. Удельная теплота плавления льда ?л = 340 кДж/r, удельная теплоемкость льда сл = 2100 Дж/(кг·0С), удельная теплоемкость воды
св = 4200 Дж/(кг·0С). Теплоемкостью калориметра и теплообменом пренебречь.
Решение. Обозначим: m – масса льда, С – теплоемкость одного металлического бруска, t – первоначальная температура бруском.
После опускания первого бруска в калориметре образуется смесь воды и льда при температуре t0 = 00C.                                                      1 балл
Уравнение теплового баланса после опускания первого бруска
.                                               2 балла
      .                                        3 балла
двух уравнений относительно температуры t, получим (учтено, что t0 = 00C):
 .                                       4 балла